√100以上 辺の比 面積比 952952-辺の比 面積比

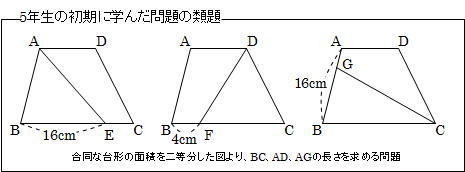
小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾

面積の公式はπ r 2 なので、 π r 2 ＝36π r ＝6（cm） 半径＝6cmなので、 直径は、6×2＝12（cm） ≪答≫ 12cm ※水面の半径を求めてからも解けるから試してみてね！ ＜前： L37 相似な立体の表面積と体積の比 の問題 『第5章 図形と相似』の復習テスト の問題 下の図のように， 辺の長さが4cm，7cmの平行四辺形ABCD があります。角Aの2等分線と辺BC の交わる点をE とするとき，三角形ABEの面積と四角形AECD の面積の比を求めなさい。（大妻多摩中学校）

辺の比 面積比

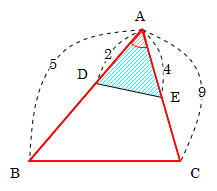
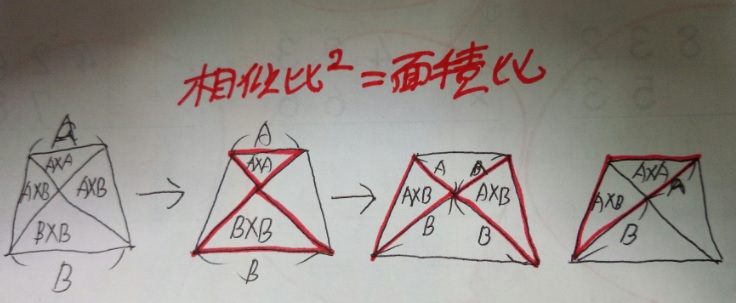
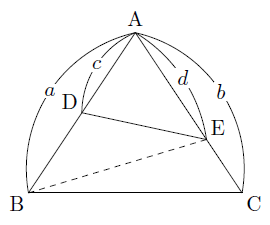
辺の比 面積比-2辺の比から面積の比を求める基本問題の逆算パターンです。 「隣辺比」 と呼ばれる解き方です。 右の図のように、 三角形abcと三角形adeで「ひとつの角（角a）が共通（重なっている）」とき、 面積の比はその共通角をはさむ2辺の積、4 2つの三角形の底辺の比が ab ，高さの比が mn のとき，面積の比は ambn になる． 5 右図6のように2つの三角形で1つの角が共通のとき，この角をはさむ2辺の比が各々 ab ， mn のとき，面積の比は

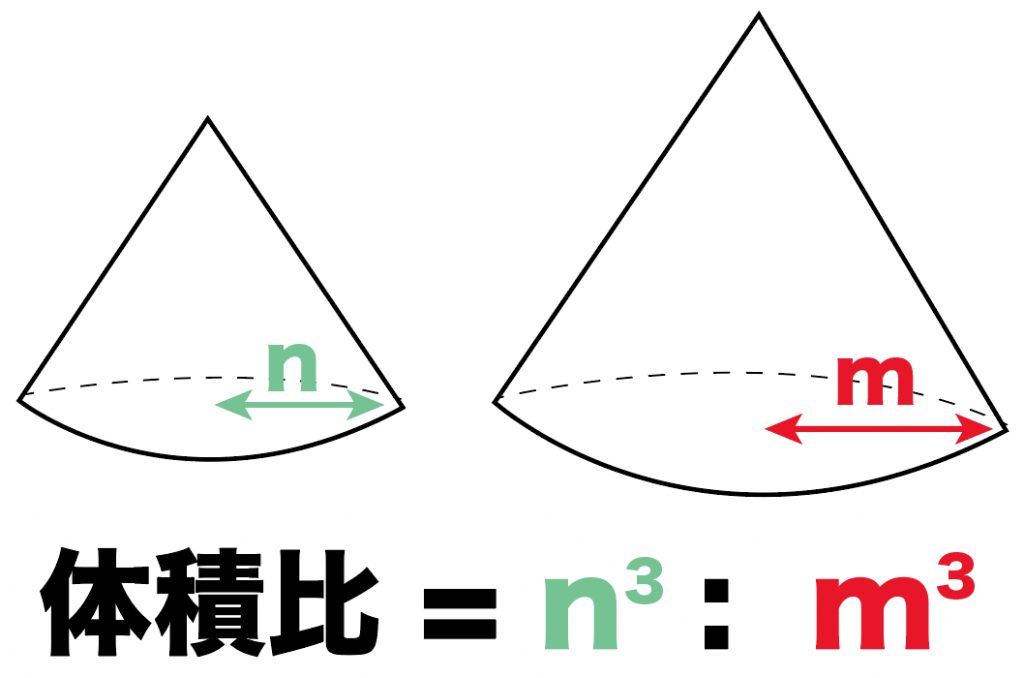
3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく

 1つ目のステップでは、 abdと acdの面積比に注目します。 隣り合う三角形の ①の型 なので、底辺の比＝3：5から面積比も3：5。 そして左側の ABDは、 ABCを8等分したうちの3つ分ですから、\( ABD\)の面積＝\(\displaystyle \frac{3}{8}S\)と表すことができます。 辺の比と連比の中学入試問題等 問題）女子学院中学 abcdは長方形。同じ印は同じ長さ。 （1）bhとidの長さの比を最も簡単な整数の比で表すと ： です （2）三角形ahiの面積は cm² （すんません、iとbの途中のaeとの交点がhどす）体積の比 1 相似な平面図形の面積 （1 時間） 〈目標〉 相似な平 面図形 比と積 関係を理解する。 問題 左の図のア，イについて， 面積が大きいのはどっち？ 相似な平面図形の相似 比，面積比について，具 体的な事象から一般的に いえることを

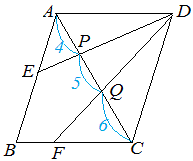
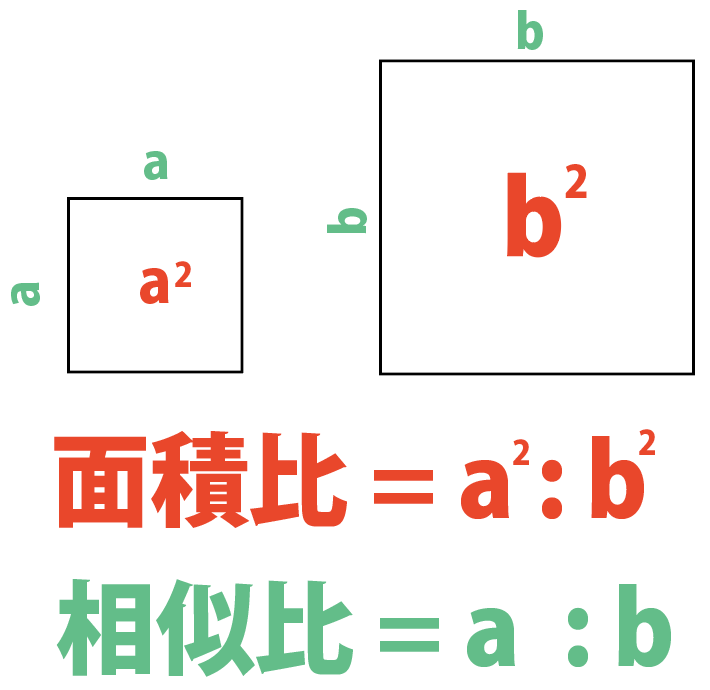
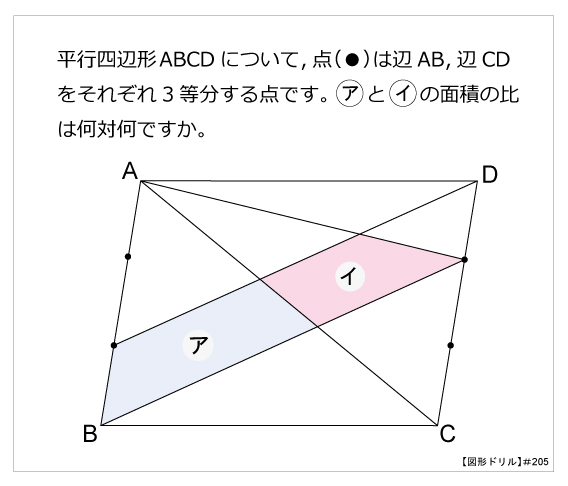
 つまり、辺の長さの比（相似比）の3乗の比が体積比に相当することを理解しておきましょう。 円錐の体積比の計算問題を解いてみよう それでは、塩水の相似比、面積比、体積比の算出に慣れるためにも、練習問題を解いていきましょう。 例題 面積比の標準練習問題 図のように、平行四辺形abcdがある。辺cdの中点とeとして、直線aeと辺bcとの交点をf、aeとbdの交点をgとする。このとき、次の問いに答えなさい。 （1） agd： bgfの面積の比を求めよ。 （2） agdと四角形gbceの面積比を求めよ。 相似比と面積比，体積比の公式の証明 4 4 倍 になる。 9 9 倍になる。 k\times k=k^2 k × k = k2 倍になる。 相似な図形（形が同じで大きさが違う図形）の面積比・体積比について解説し

辺の比 面積比のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	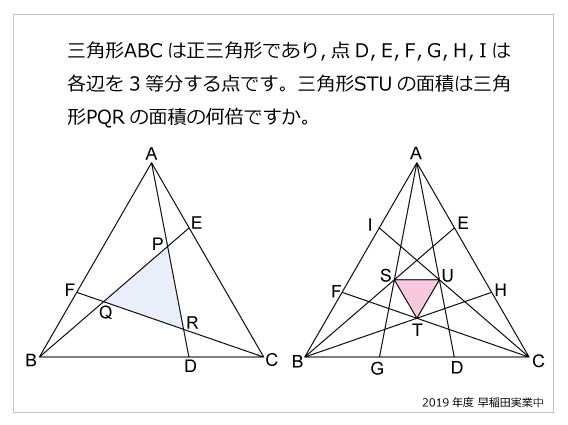平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	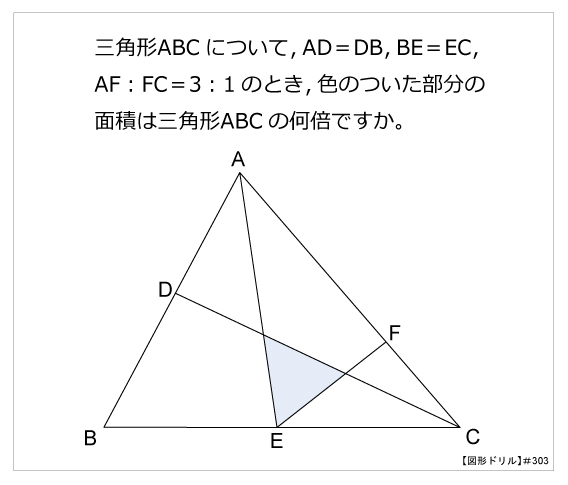平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	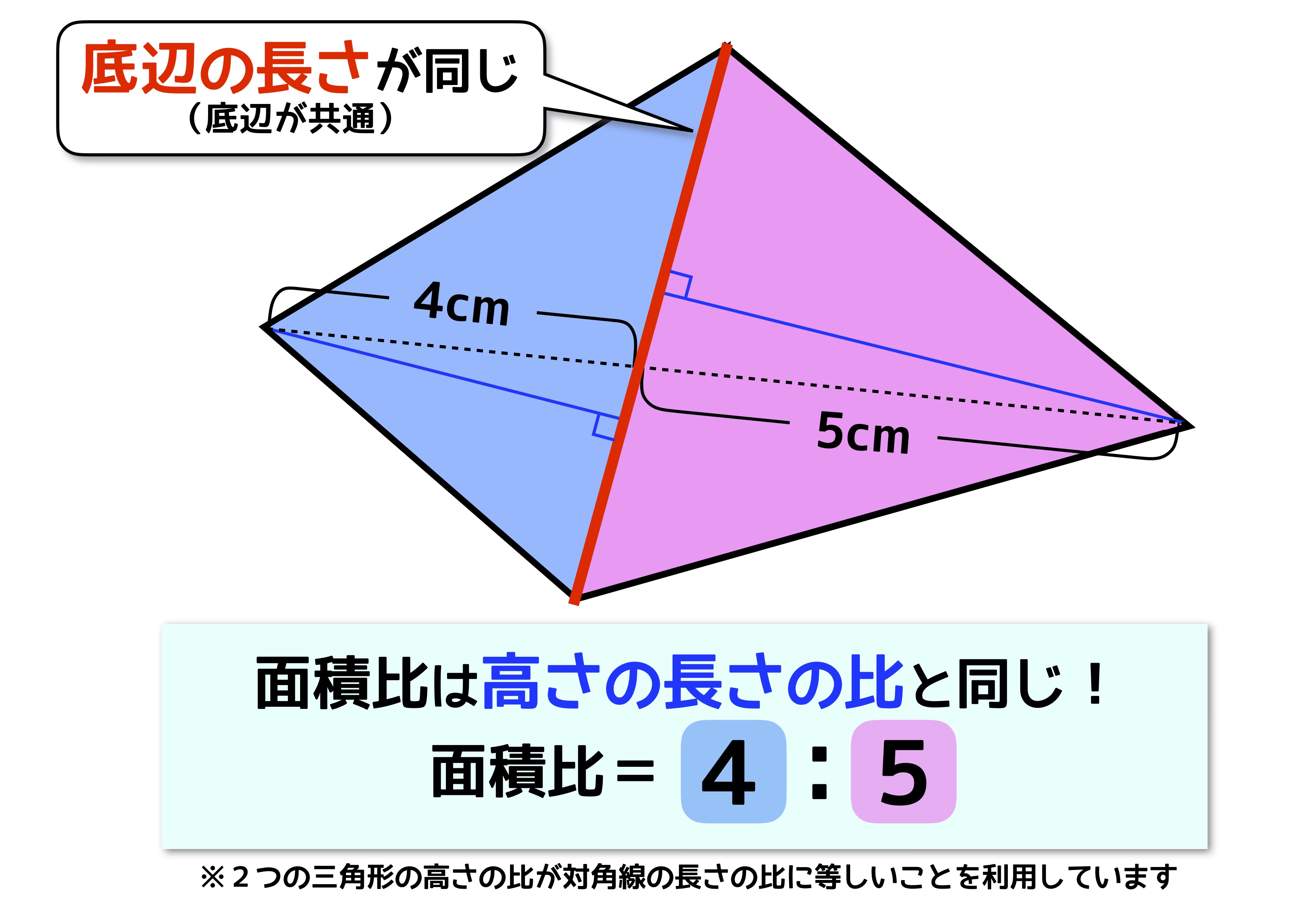平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	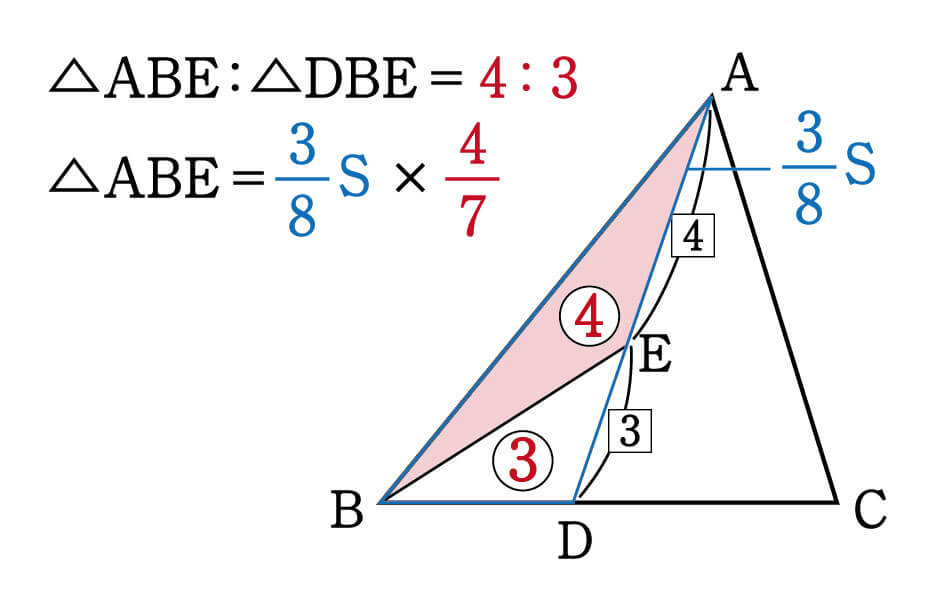平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	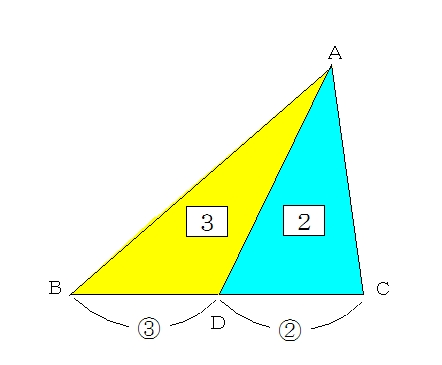平面図形をマスター 三角形の面積比 応用編その３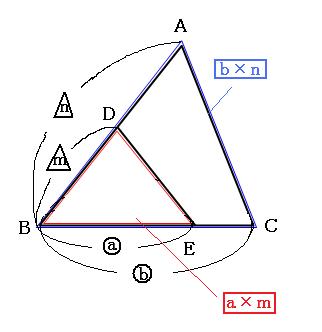
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３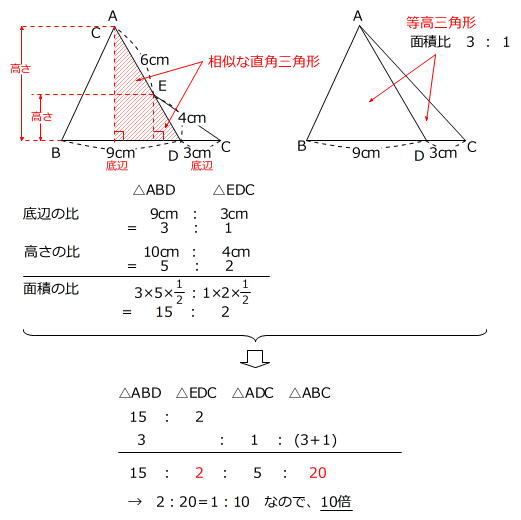
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	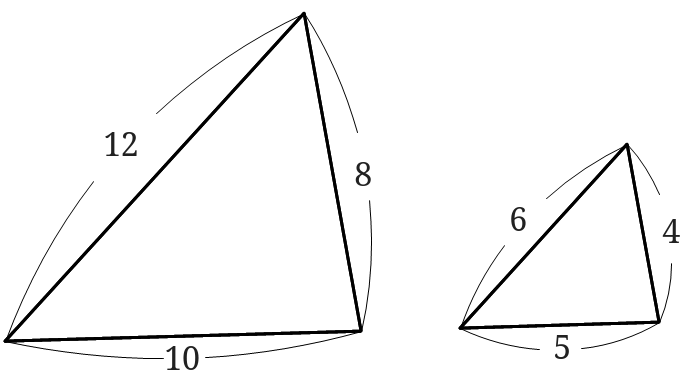平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３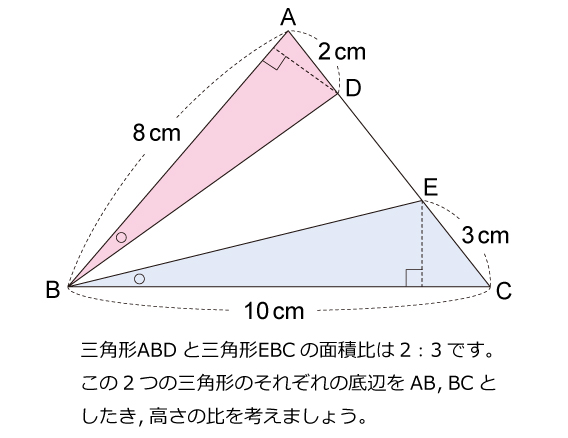
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	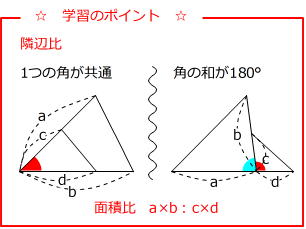平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	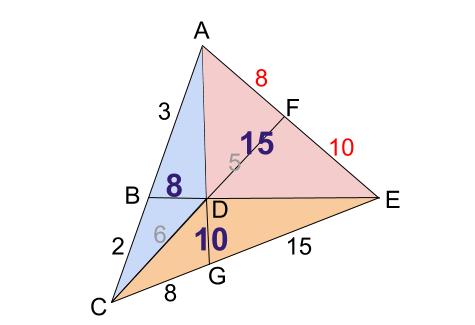平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	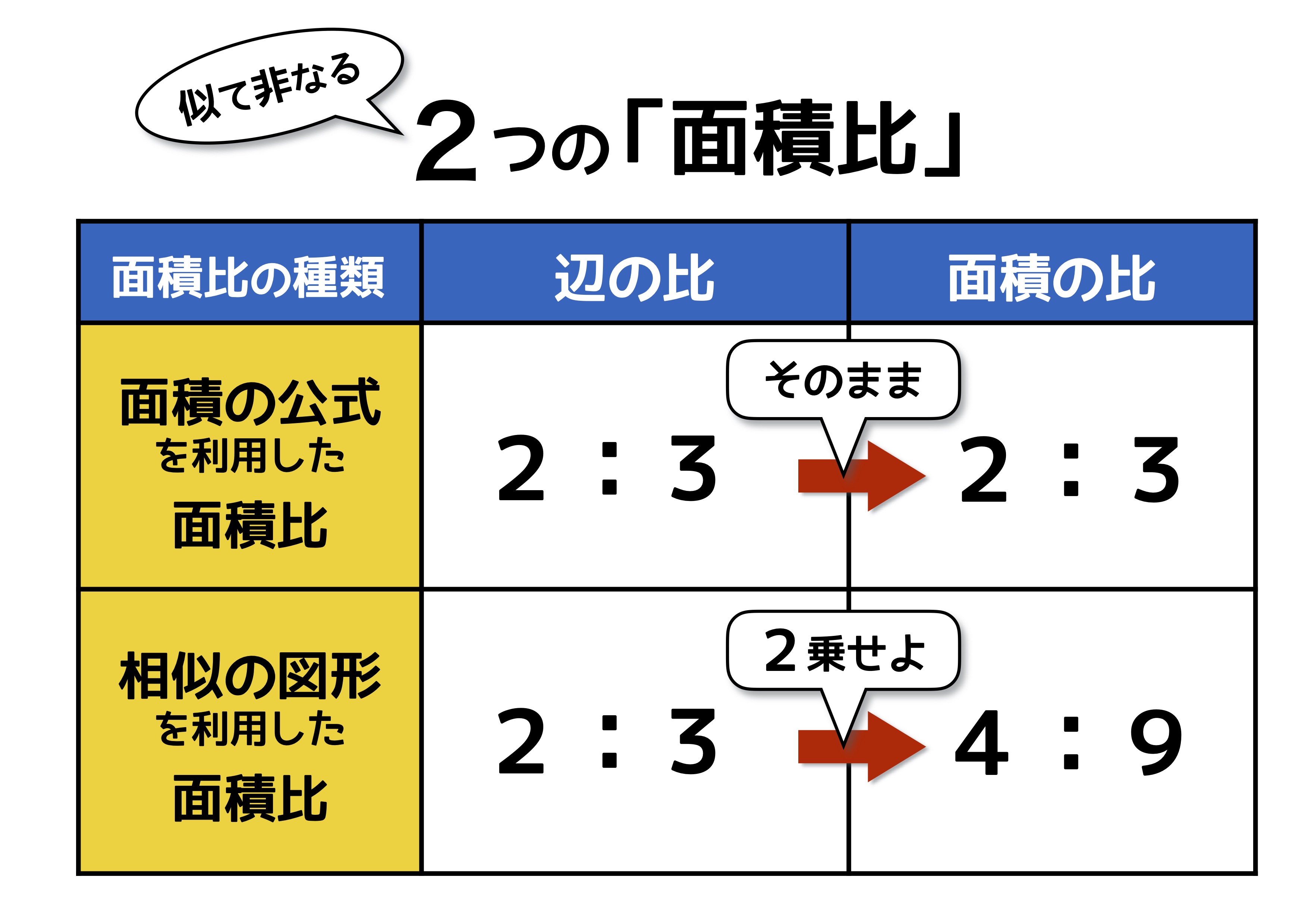平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	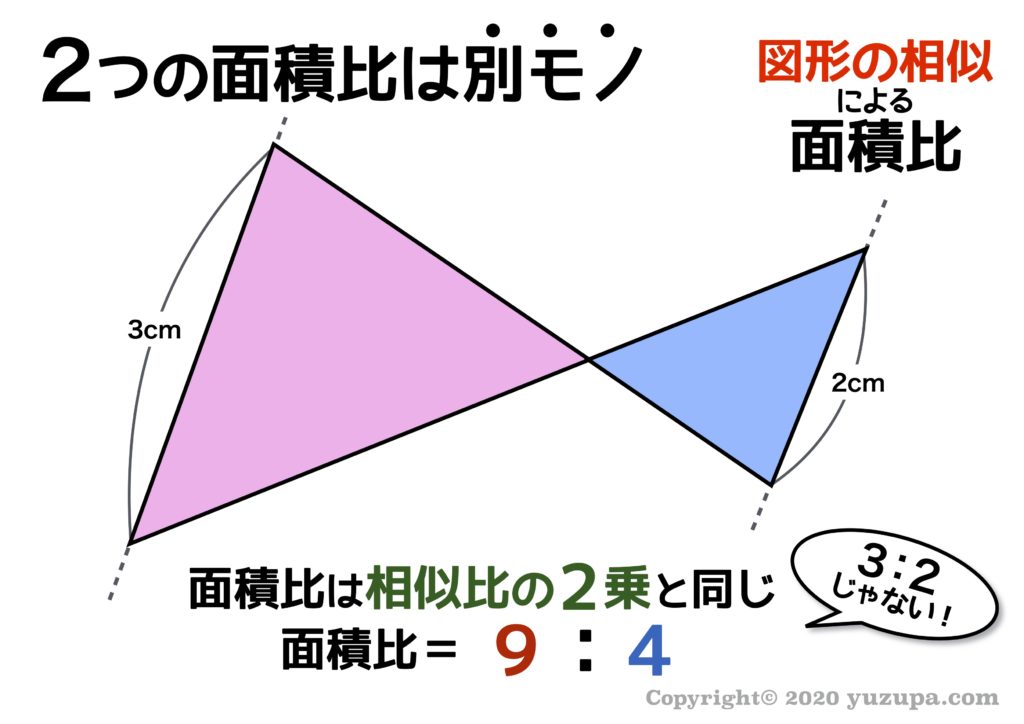平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	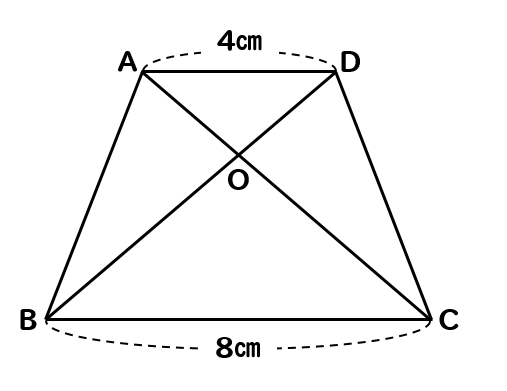平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	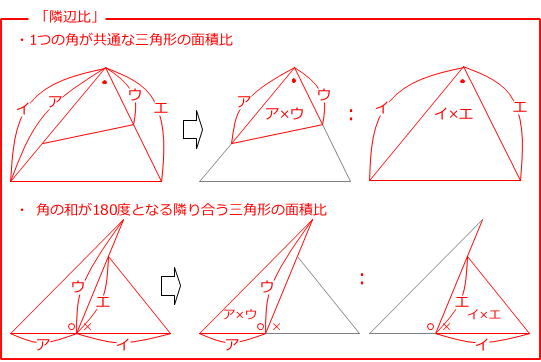平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３	平面図形をマスター 三角形の面積比 応用編その３
平面図形をマスター 三角形の面積比 応用編その３	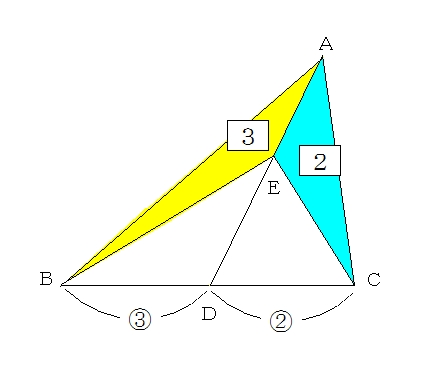平面図形をマスター 三角形の面積比 応用編その３

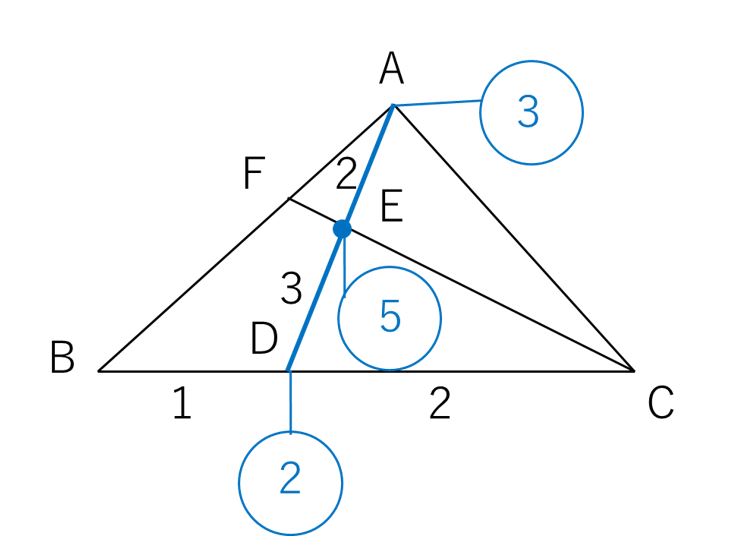
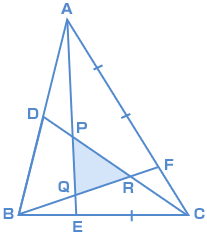
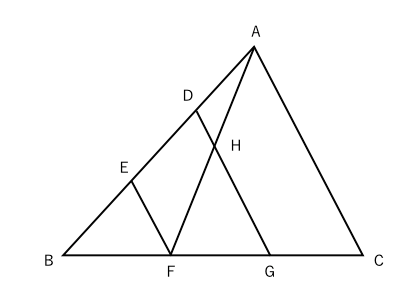
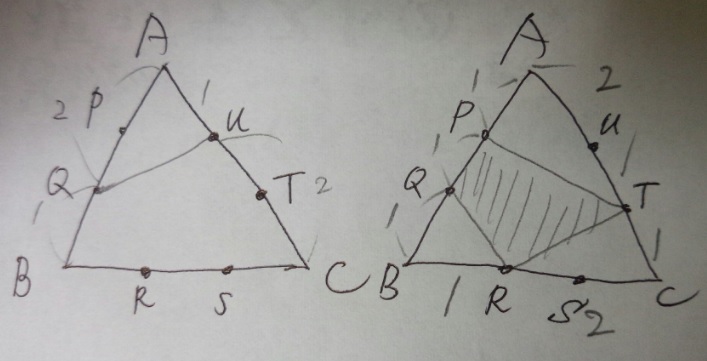
 2つの異なる比を「合成」して、「連比」を作ったわけです。 この連比を使えば、母と弟を比較して正解を導き出せます。 続いて、比の合成を面積比の問題に適用してみましょう。 ABCがあり、辺BCを3：5にわける点がD、ADを4：3にわける点がEとなってい いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq ： qr ： rf ＝ 2 ： 2 ： 1 に注目します。 次に、cr ： rp ： pd ＝ 2 ： 2 ： 1 に注目して、

Incoming Term: 辺の比 面積比, 辺の比 面積比 関係,