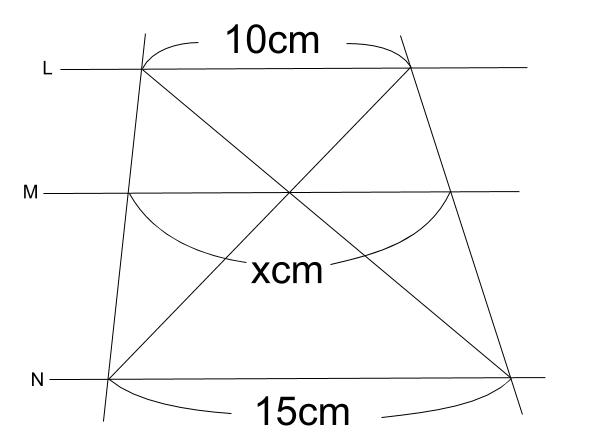
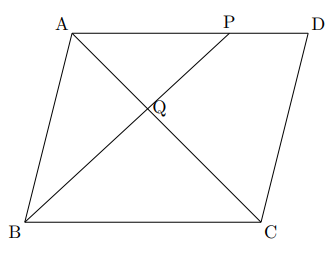
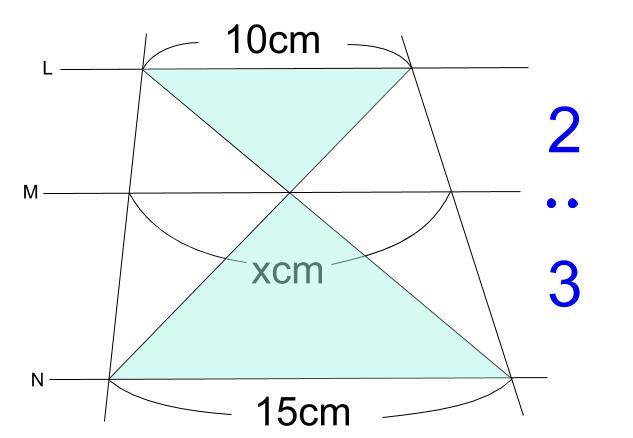
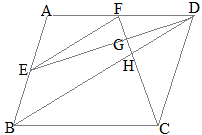
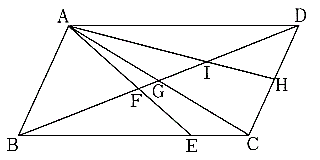
こんにちは。今回は神奈川県の入試問題より, 平行線と線分の比に関する問題です。それではどうぞ。 図において, 四角形abcdは平行四辺形である。また, 点eは線分bc上の点であり, 三角形abeは正三角形である。さらに, 線分abの中点をfとし, 線分aeと線分cfとの交点をgとする。線分の平行四辺形分割(コ)) 線分の平行四辺形分割(コ) (図) 命題29 (作図線分の平行四辺形外分割(コ)) 線分の平行四辺形外分割(コ) (図) 命題30 (作図外中比) (図) 命題31 (直角三角形の辺上の相似な図形) 平行線と線分の比で下の写真の三角形の比が 22+3=25 とあったのですがこの式はいったいどういう理屈で出てきたかわかりません 何故22という 比が出てきて更に3を足すのですか、何
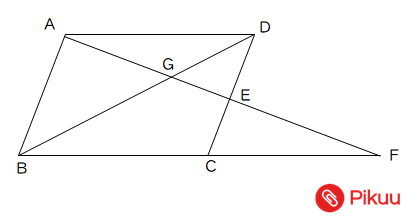
次の図の平行四辺形abcdにおいて Ab Efとする このとき Yahoo 知恵袋
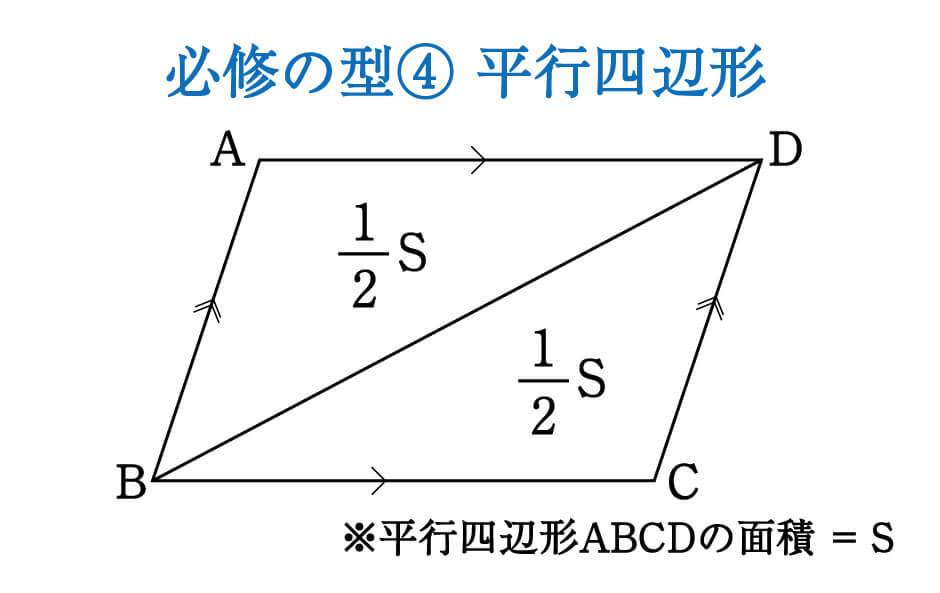
線分比と面積比 平行四辺形
線分比と面積比 平行四辺形-反射テスト 平面図形 線分比・面積比 平行四辺形 まとめ 02 1 平行四辺形abcd がある 辺ad を1 2 に内分する点をe;辺bc の中点をf とし; no1 線分比に拘り過ぎ! ∠agbと∠dgeは対頂角で等しい 平行四辺形よりab平行deより abg相似 dgeより ag ge=32 (1)



1
平行線と線分の比 6 0 0 Loading (view fulltext now)平行線と比の利用、辺の長さを求める問題をパターン別解説!←今回の記事 木の高さを求める方法について解説! 中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比!相似比の練習問題(平行四辺形4) 問6.ab¥dc,ad¥bc,be:ec =2:1 のとき fbe の面積: fda の面積 =( ):( ) fbe の面積: dec の面積 =( ):( ) 問7.平行四辺形abcd の辺ab,ad の中点をそれぞれe,f とし対角線bd と線分cf の交点 をg,線分cf と線分ed の
無料講座の解説資料 訂正後中3数学講座第5章 図形と相似(13)平行四辺形と線分比 基本問題pdf 有料講座をご覧いただくにはログインが必要です。 ユーザー登録がお済みの方は、 ログイン 。 ユーザー登録がまだの方は、 ユーザー登録(無料) を辺の比・面積比・相似 範囲:中3相似 難易度:★★★★☆ 得点 /10 出典: 16 年度 東京都 四角形 abcd は平行四辺形である。点pは,辺 ab 上にある点で,頂点 a,bのいずれにも一致しない。頂点 aとcを結んだ線分と,頂点 dと点平行線と台形中3数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・平行線で三角形を作り、線分の比を利用する 完璧じゃなかったら授業動画を見よう やる気先生の授業動画 326K subscribers
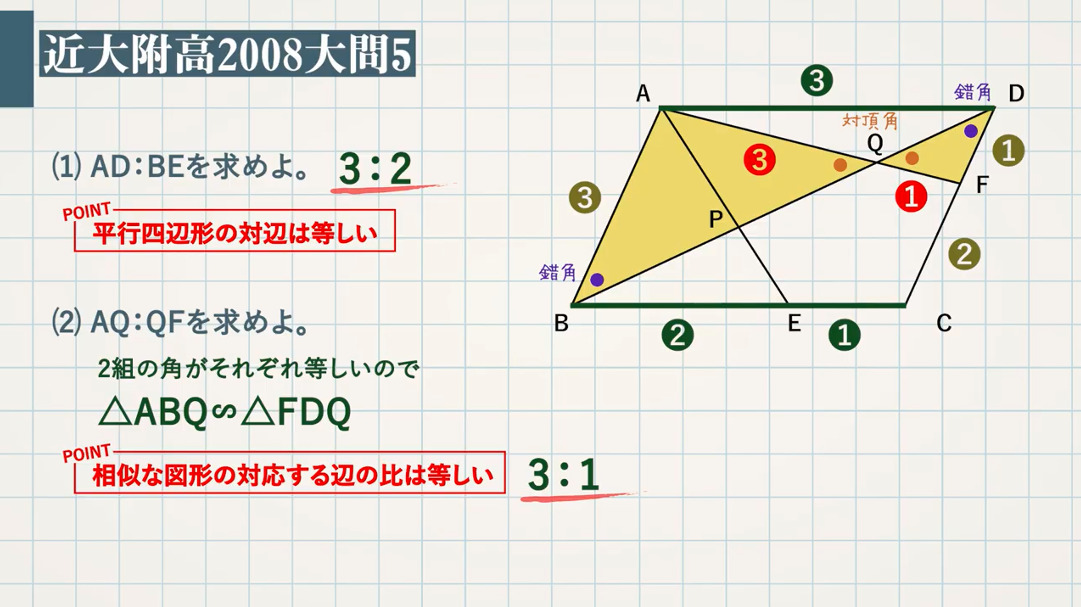
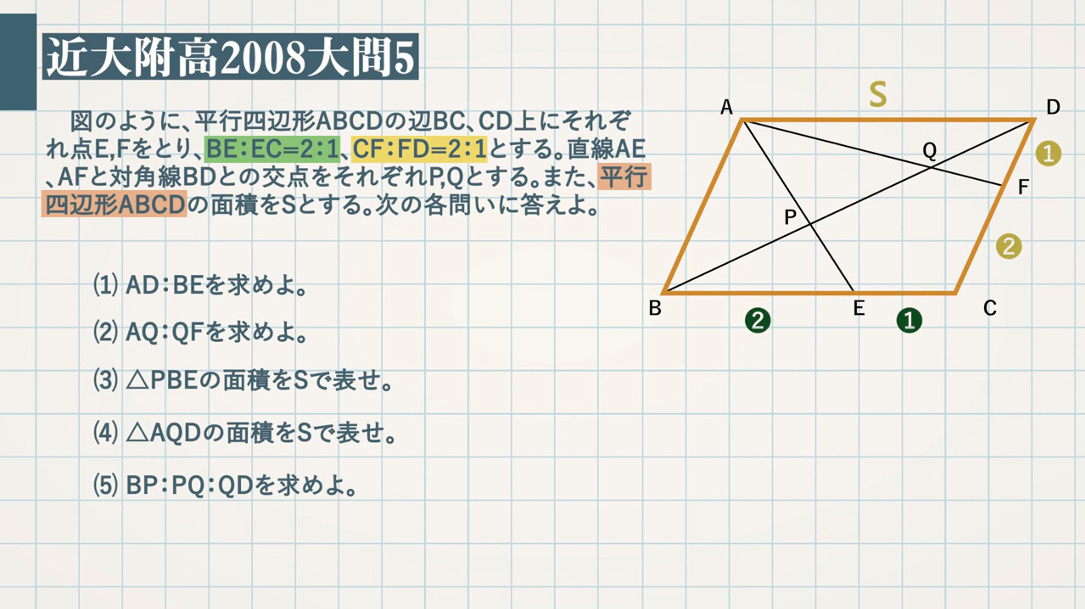
さらにef とgh との交点をi とする (s 級2 分50 秒;POINT:平行四辺形の対辺は等しい $\rm BEEC=21$ より、$\rm ADBE=\textcolor{red}{32}$ (2) $\textcolor{green}{\rm AQQF}$ を求めよ。 図の対頂角、錯角の $2$ 組の角がそれぞれ等しいので、$\textcolor{blue}{\rm ABQ∽ FDQ}$ POINT:相似な図形の対応する辺の比は等しい反射テスト 平面図形 線分比・面積比 平行四辺形 まとめ 01 解答解説 1 平行四辺形abcd がある 辺ad の3 等分点を図のようにe;f とする (s 級40 秒;



授業実践記録 数学 新しい 定理 とその活用 啓林館



平行線と線分の比 中学3年 数学クラブ
10 『相似』! なら「対応する辺」と「順番」さえ合っていればよい ① 2つの三角形が『相似』だった場合、ある辺の長さを求めるための表現は 実は自由です このあと「平行線と線分の比」や「方べき」などで 「この辺」:「この辺」は「この辺イ 三角形の相似条件などを基にして図形の基本的な性質を論理的に確かめること。 ウ 平行線と線分の比についての性質を見いだし,それらを確かめること。 エ 基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の関係について理解すC 級4 分) (1) ge eb



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3011 Pdf



中学数学 平行四辺形の証明問題を徹底解説 数スタ
上図のように平行四辺形abcdがあります。 線分adとCBは平行四辺形の対角線です。 今、線分cd上に点Eを3:1にとり、線分beを引きました。 この時、 (三角形①の面積) : (三角形②の面積) : (三角形③の面積) の比を求めて下さい。線分比→平行 問題(3 学期) 次の文は,三角形と線分の比についての定理である。( ) をうめよ。 abc で,辺ab,ac 上の点を,それぞれp,q とする。 (1) pq // bc ならば, ap:ab=aq:( ア )=pq:( イ ) (2) ap:pb=aq:qc ならば,pq // ( ウ ) 解答欄 ア イA 級1 分40 秒;
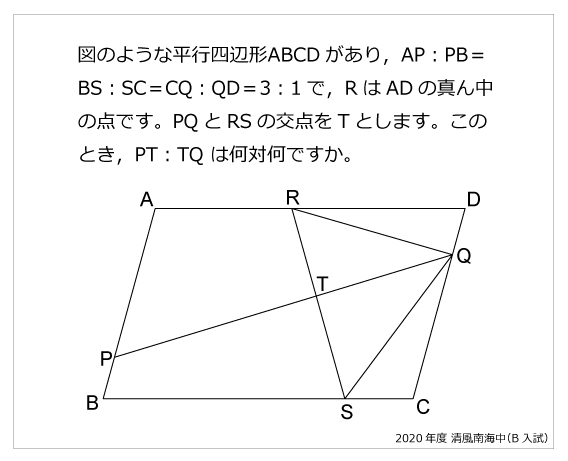



今年の1問 年清風南海中 平行四辺形と比 算数星人のweb問題集 中学受験算数の問題に挑戦



相似な図形の比の問題です 次の図の平行四辺形abcdで 指定 Yahoo 知恵袋
例題図の平行四辺形において、辺 $\textcolor{green}{\rm BC,CD}$ をそれぞれ $\textcolor{green}{21}$ に分ける点を $\textcolor{green}{\rm E,F}$ とし、対角線 $\textcolor{green}{\rm BD}$ と $\textcolor{green}{\rm AE,AF}$ の交点をそれぞれ $\textcolor{green}{\rm P,Q}$ とします。 このとき、次の問いに答えなさい。 平行四辺形と線分比>>中学三年生() 分数と比が苦手な人のための「 / 法」() 相似と線分比 >> 中学3年生() "never"の覚え方=>中学3年生() 挑戦というゲーム()相似・線分比と面積比 レベルaの25題 問1 右の図でabとcdが平行なとき、ア〜エの長さを求めなさい。 問2 右の図でabとcdが平行なとき、ア、イ、ウの長さを求めなさい。 問3 右の図形はある土地の1:00の縮図です。この土地の実際の面積が何m2



1



平行四辺形と比 教遊者
関連記事 (21都立西)平行四辺形の難問証明 丁度良い角の二等分線公式(14年度沖縄県) 円周角と半径(中3円周角 証明プリント) 45(02年度茨城県改題) 範囲が大分削除された(オリジナル)た,線分 ae ,bd の交点を f とする。対角線 ac 上に,fh™bc となるような点 h をとるとき,次の問いに答えよ。 〔高知学芸高〕 ⑴ bf:fd を求めよ。 ⑵ fh:bc を求めよ。 ★ ⑶ aeh と平行四辺形 abcd の面積比を求めよ。 4 次の問いに答えよ。 平行四辺形中の線分比問題は相似で解決 相模原市中央区矢部で数学を得意になってもらうための塾・青木学院です。 今日はテストゼミの解説授業日でした。 最後のいわゆる「合否判定の参考」となるデータを配布しました。 あくまで過年度の先輩方と



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



高校入試数学 連比の対策問題 中学生勉強サイトあかね先生
線分XEと線分DGは平行 じゃから、平行と線分比の関係から、 AX XD = AE EG が言えるわけじゃな 同じものじゃが、分数の形で書いておくと、 mathjax A X X D = A E E G ・・・式(1) となるわけじゃ(これを、式(1)とするかのぉ) 数学おじさん もう1つ、別平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\) が平行相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




中3 19 2 平行四辺形と相似 Youtube
右図の平行四辺形 においabcd て, の中点をE, と の交ad ec bd 点をFとするとき と , fde fbc 問題番号問いの面積の比を求めなさい。 12 正解 1:4 誤 答 例 つまずき原因 分析と解消 1 無解答 2つの三角形が相似であることに気が付かな30ページ い。C 級11 分) (1) ag gf を求めよEc とdf の交 点をh;




A8 Sqrt8right Abcd Ab6c Descubre Como Resolverlo En Qanda




東京都立高校19年共通試験 問題4 平行四辺形 過去問 数学 高校受験講座 東京先生
3 平行線と線分の比 「平行線に直線が交わるとき、その交点の間の比は等しくなる」ことを次のように 証明した。直線l,m,nが平行であるとき、かっこに当てはまる語をうめよう。 点aを通り、直線a′に平行な直線を引き、それと直線m,nの交点をd,eとした。B 級2 分50 秒;FdData 高校入試:中学数学3 年:相似・平行線 相似の証明・長さ:2 組の辺の比とその間の角/相似な三角形→長さ/2 組の角/ 平行線と線分の比:平行線 /三角形と平行線/平行四辺形と平行線/平行線と相似の証明/ 中点連結定理:長さを求める/
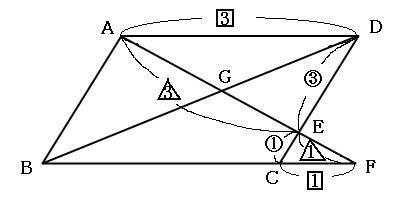



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ



次の図の平行四辺形abcdにおいて Ab Efとする このとき Yahoo 知恵袋
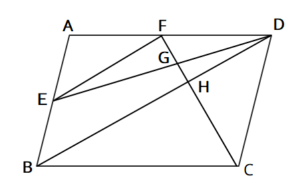
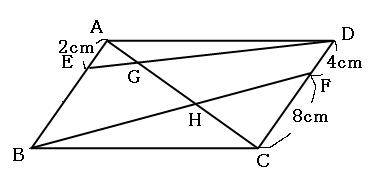
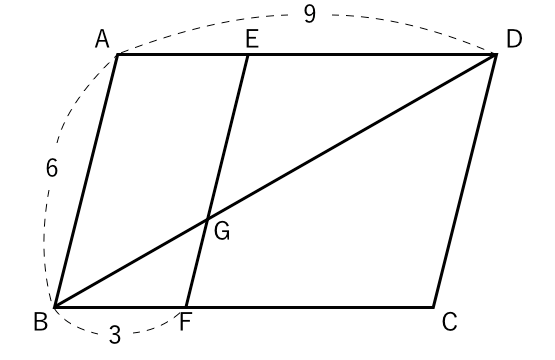
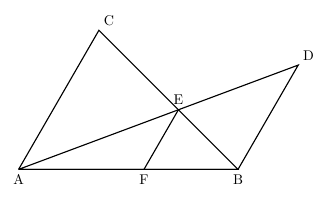
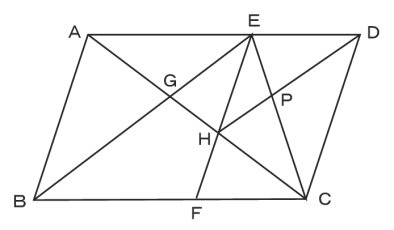
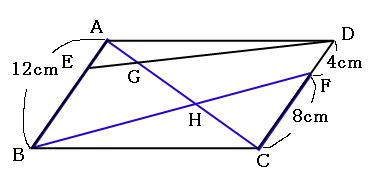
この青いチョウチョは、辺abと辺cfが平行なので(←四角形abcdが平行四辺形だから)、三角形habと三角形hcfが相似になっています。 相似比を求めると、 辺ab辺cf=12cm8cm=32 よって、辺ah辺chも32です。 ここで線分acだけ抜き出して書いてみます。右の図のように,平行四辺形 abcd がある。辺 ab の中点を e とし,点 e を通り線分 bd に平行な直線と辺 ad との交点を f とする。また,線分 cf と線分 ed, bd との交点をそれぞれ g, h とする。 このとき,次の(1),(2)の問いに答えなさい。 (1) 略数学35章図形と相似「平行線と線分の比」<準備問題> 組 番 名前 1平行四辺形の定義を書きなさい。 2四角形が平行四辺形であるための条件が3つ書いてあります。あと2つ,条件を書きなさい。 ・2組の向かい合う辺がそれぞれ平行である。



高校入試対策数学 面積比に関する対策問題 Pikuu



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
「平行線と線分の比の定理」の問題の解き方 管理人 5月 5, 三角形の相似条件と証明問題の解き方 図形を拡大・縮小したものを相似といいますが、三角形の場合、相似であることを証明するための条件があります。 平行線の線分比の性質を使った問題です。 図形を見てどことどこが相似になりそうかわかるようになると良いですね。 次の四角形abcdが平行四辺形 当然、平行四辺形である、長方形、正方形、ひし形でも同様のことが言えます。 今回は例が非常に簡単ですが、結構使える場面が多いので覚えておきましょう。 そこそこ見る3つの線分の比を求めるパターン 別々の辺の比は揃えることができます。



平行四辺形を分ける面積比の求め方 算数解法の極意



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
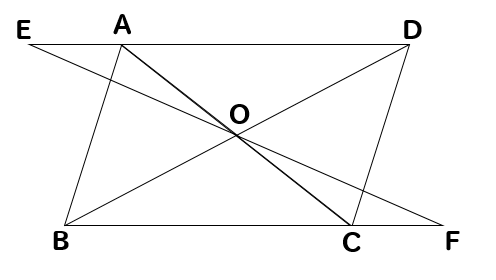
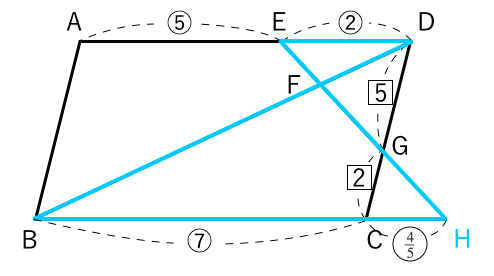
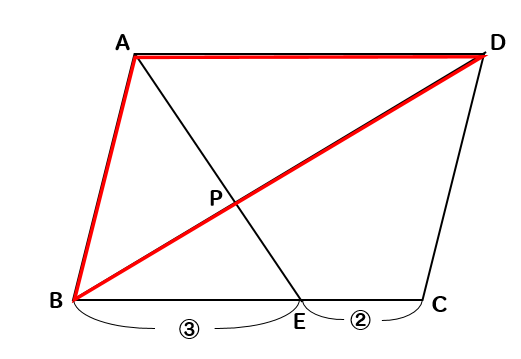
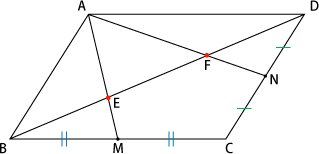
Ex) 平行四辺形abcd において、辺bc の中点をe 、辺 cdを2:1の比に内分する点をf 、辺 ad を1:3の比に内分する点を G とし、線分 EG と線分 BF の交点を P とする。



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




3数 平行四辺形と線分の比 Youtube




四角形abcdが平行四辺形 Bfが Abcの二等分線 Abfの面積が6cm のとき Clear




無料 中3数学 標準問題 解答プリント 328 図形の相似3 線分の比




線分比と面積比 鷗友学園女子 H18大問3



中3数学12 図形の相似3 線分の比 発展問題プリント 問題 328



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



1



攻略法 平行四辺形と面積 数樂管理人のブログ



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




Abcd A M1 D Descubre Como Resolverlo En Qanda



2




質問させていただきます Ab Ad 2 3である 三角形apqの面積と平 Okwave



平行四辺形と比 教遊者



平行四辺形の面積比の問題 解き方を教えてください Yahoo 知恵袋




相似 平行四辺形と面積比の問題を徹底解説 数スタ




相似の利用 01 平行四辺形と線分の比 Youtube



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ



平行四辺形と線分比 中学三年生 ニャース滝の 猫が長靴をはいたなら



今月の問題 平行四辺形



平行線の線分比の問題の解法 夢を叶える塾



平行四辺形abcdにおいて対角線の交点をo 辺bcの中点をm 線分am Yahoo 知恵袋




相似 平行四辺形と面積比の問題を徹底解説 数スタ
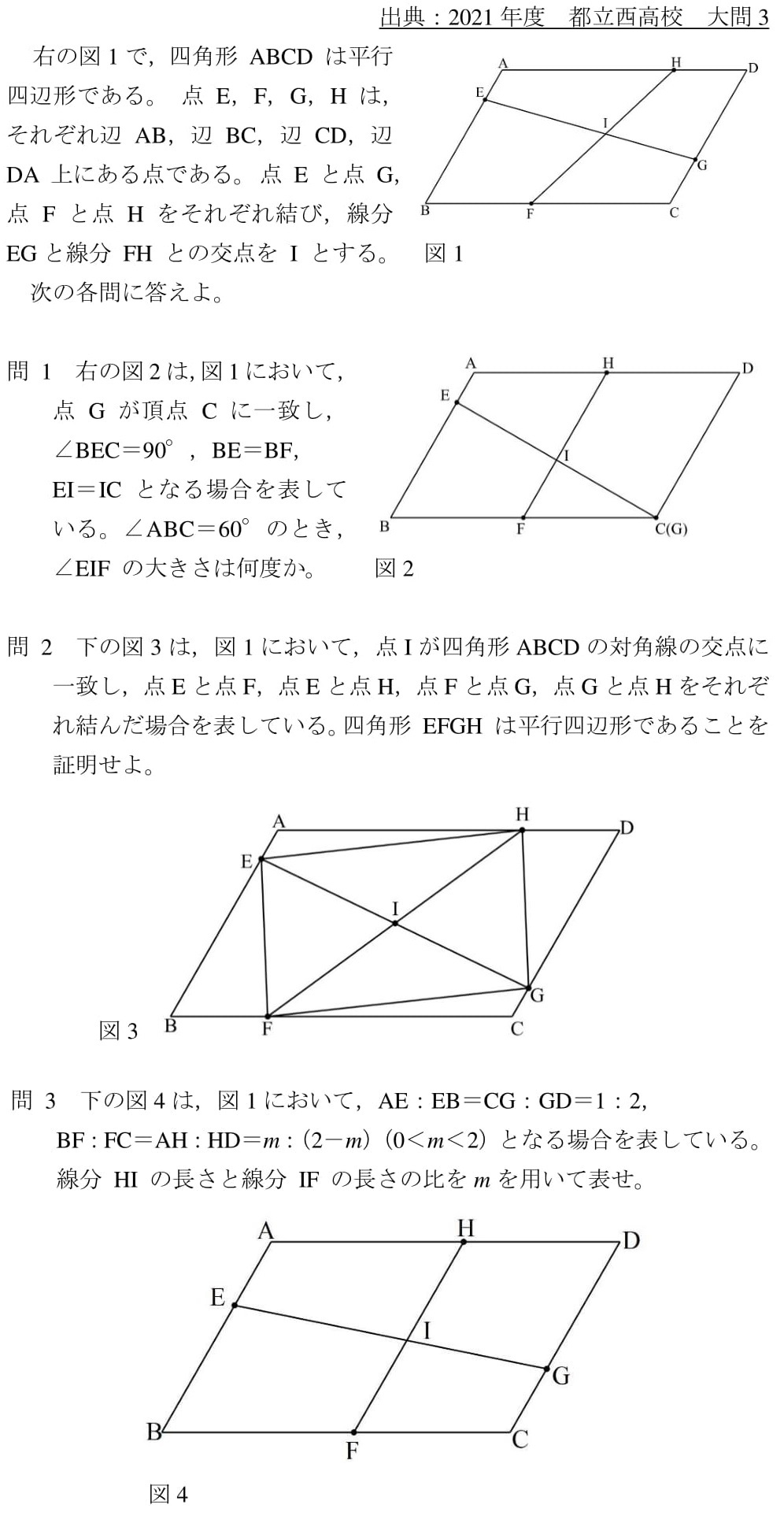



21都立西 平行四辺形の難問証明 高校入試 数学 良問 難問
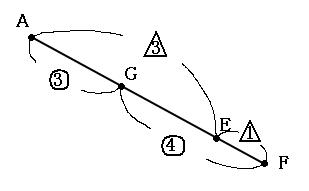



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




中3数学 相似と線分比1 平行四辺形 Youtube
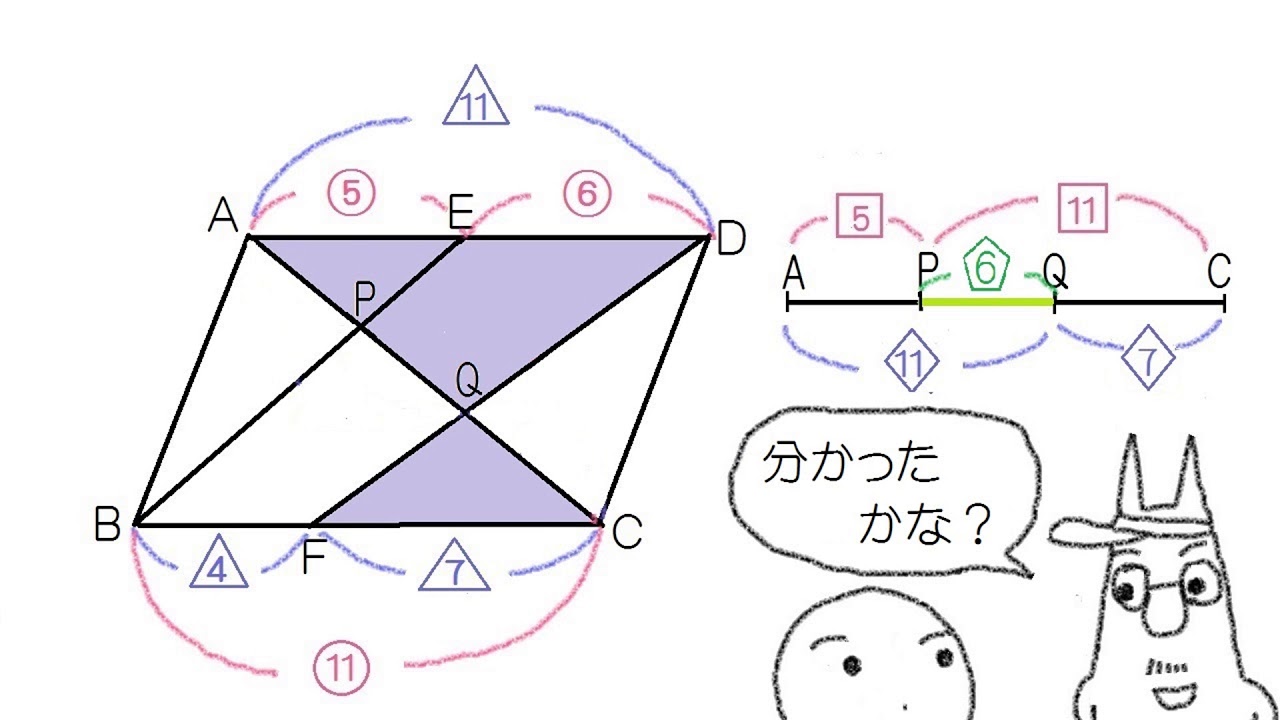



中学3年生 数学 相似 平行四辺形の対角線の線分比 Youtube



1
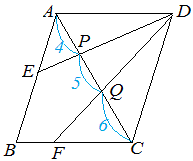



面積比



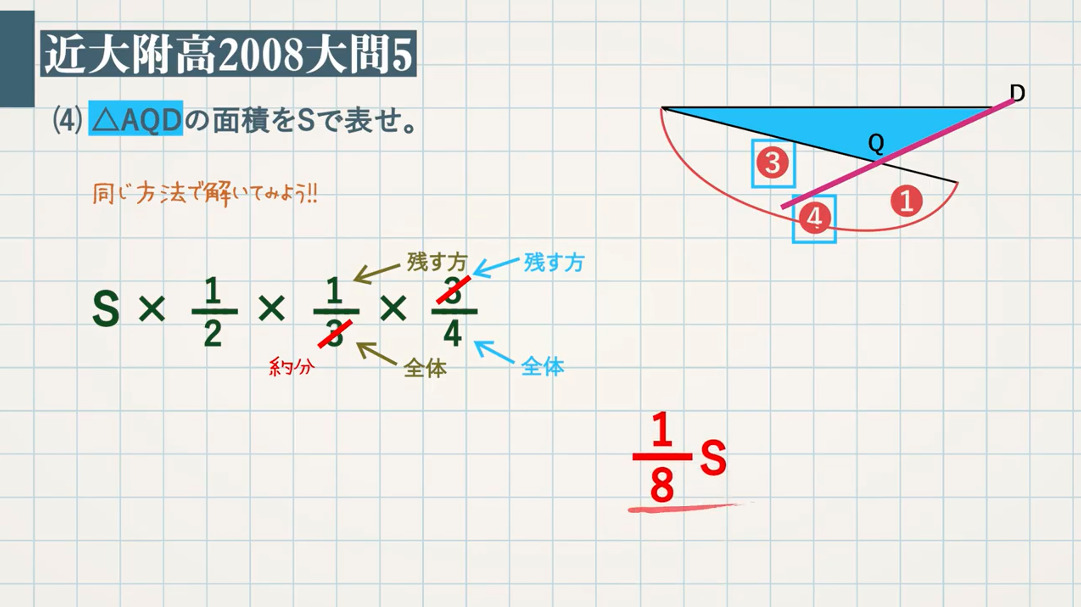
相似 平行四辺形と面積比の問題を徹底解説 数スタ



1



平行四辺形と比 教遊者
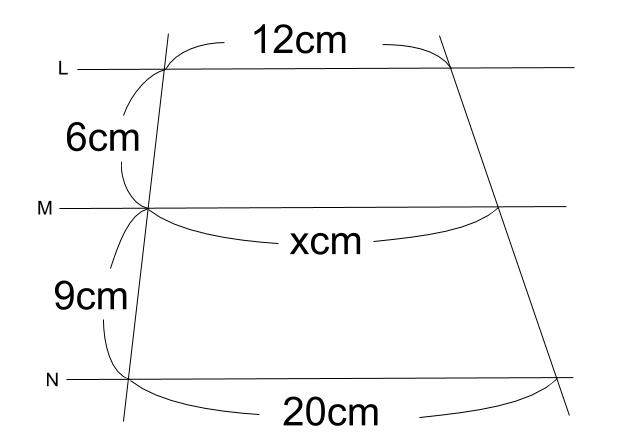



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



平行性変形でのベクトルの小手技




線分の比と面積比の問題です Fg Gcを求めよ Clear




線分比
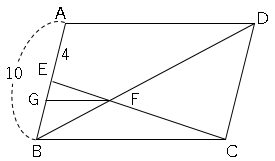



平行四辺形の性質を利用した辺の長さを求める問題 数学の要点まとめ 練習問題一覧



中学3年の数学 平行線と線分の比の利用 次の四角形abcdは 平行四辺形 Yahoo 知恵袋



相似図形 高校入試問題




図形問題 平行四辺形abcdにおいて E Fはそれぞれ辺bc Cdの中点であ 数学 教えて Goo




北辰塾 情報局 直撃 中学入試問題 第65回 攻玉社中 線分の比と面積の比



攻略法 平行四辺形と面積 数樂管理人のブログ




平行四辺形の問題です 平行四辺形abcdがあります 辺abを2 3に分 数学 教えて Goo



ややこしや 線分の比 と 面積の比 名寄 算数数学教室より




Ac Be E 5cn Descubre Como Resolverlo En Qanda




平行四辺形と線分比 中3数学 図形と相似13 Youtube



平行四辺形と線分比 中学三年生 ニャース滝の 猫が長靴をはいたなら



基礎学力アップシート 3年生 平行四辺形の辺の比を考えよう
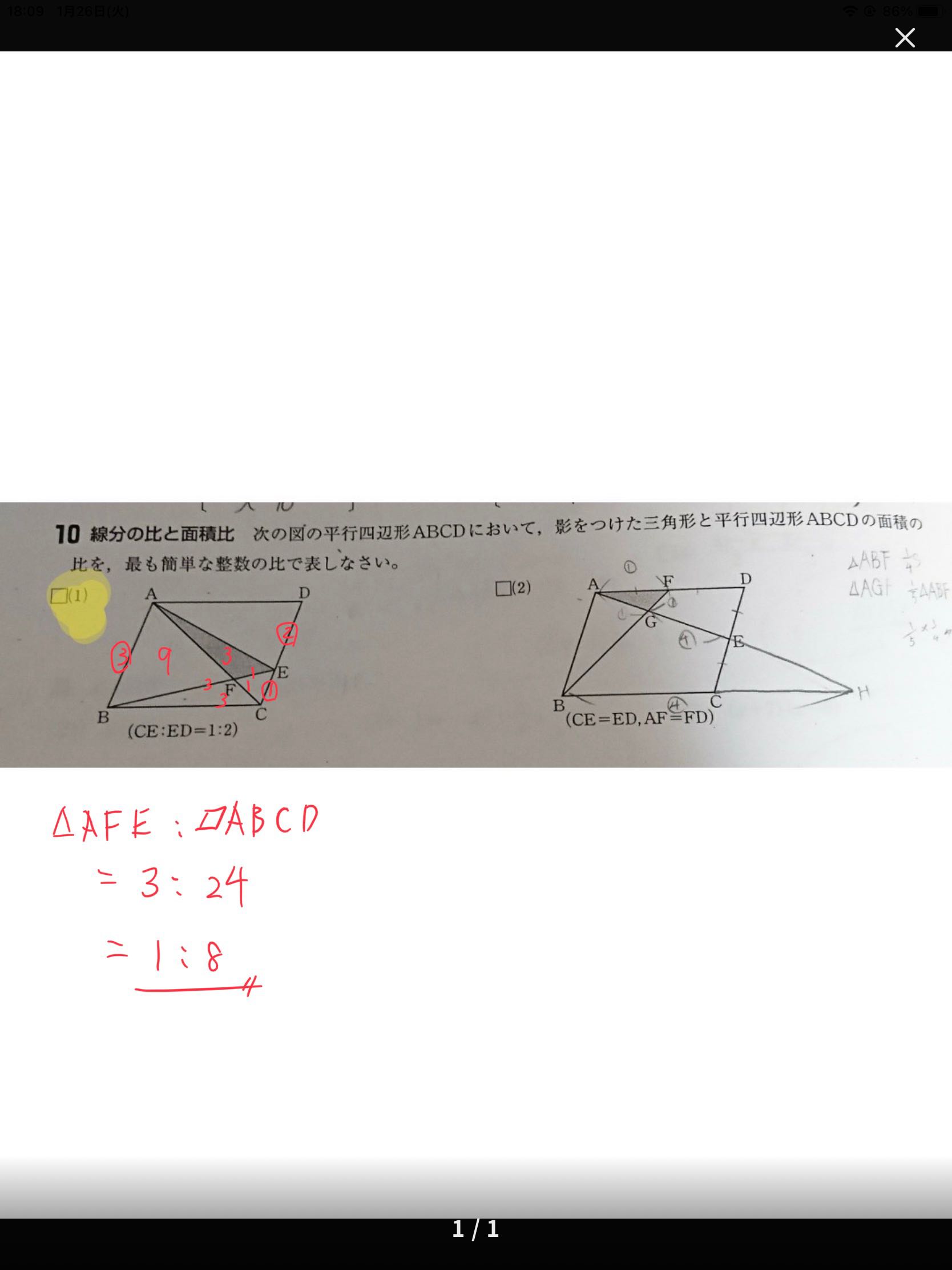



U 10 Abcd Abcd 1right D Descubre Como Resolverlo En Qanda




高校入試対策数学 面積比に関する対策問題 Pikuu




中3数学 図形と相似23 平行線と線分の比 比の合成 連比 すべて無料 星組の中学数学講座
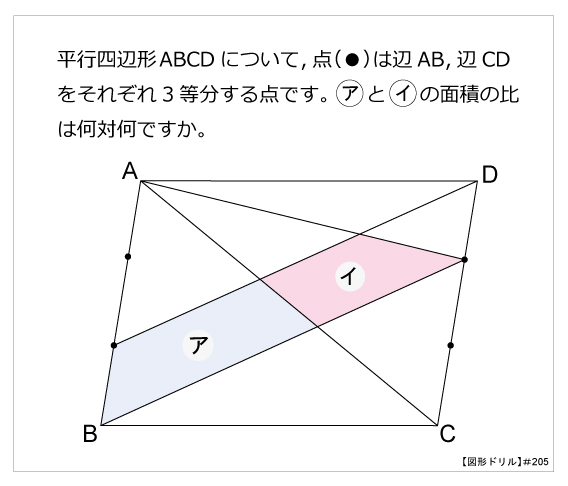



図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
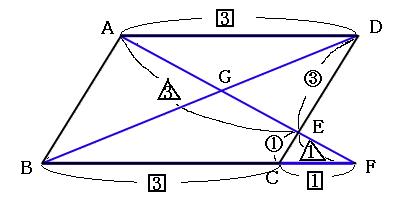



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ
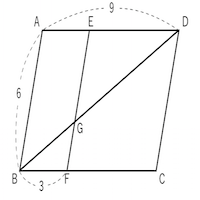



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




中学受験算数 平行四辺形の面積を求める問題 Okwave



平行四辺形の性質の利用2




相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



平行四辺形abcdは Ad 7 6cm Ab 5cmである Aの二等分線が辺 Yahoo 知恵袋



北辰塾 情報局 直撃 中学入試問題 第97回 法政大第二中 相似 平行四辺形の中の三角形




高校入試 平行四辺形と線分の比 Youtube




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



平行四辺形と比 教遊者




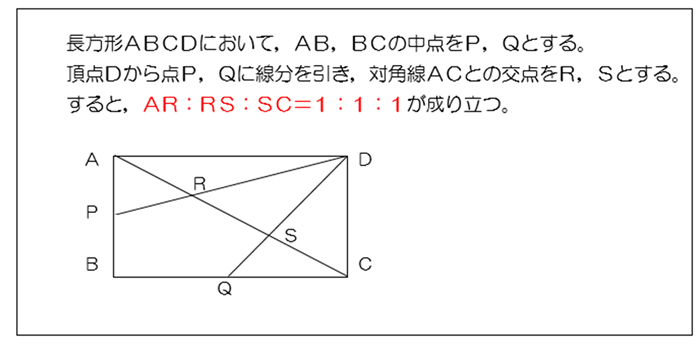
線分比 長方形内の平行四辺形 アットランダム ブリコラージュ 転ぶな 風邪ひくな 義理を欠け 長寿の心得 岸信介 食う 寝る 出す 風呂 在宅生活4つの柱




平面図形をマスター 三角形の面積比 応用編その2




算数図形編 面積比 線分比 相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ
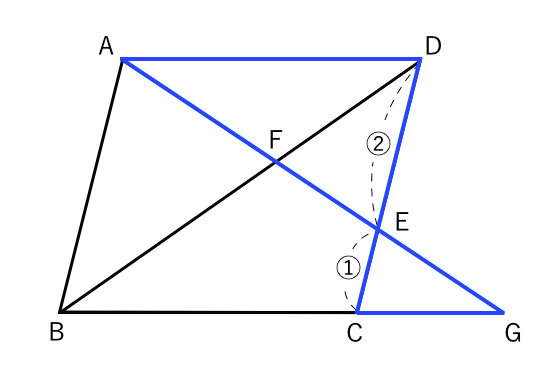



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
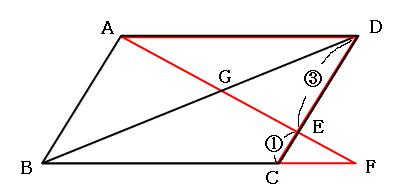



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




勉強しよう数学 10月 17




Dfeの面積と平行四辺形の面積比の問題です Clear




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



図形問題が驚くほど得意になる基本問題とは あおぞら塾
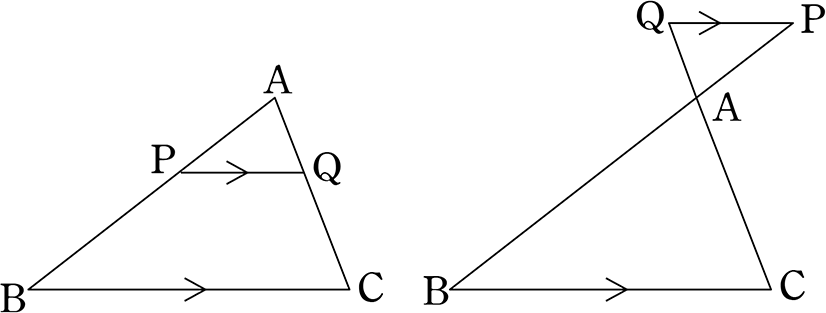



中学数学 図形の相似
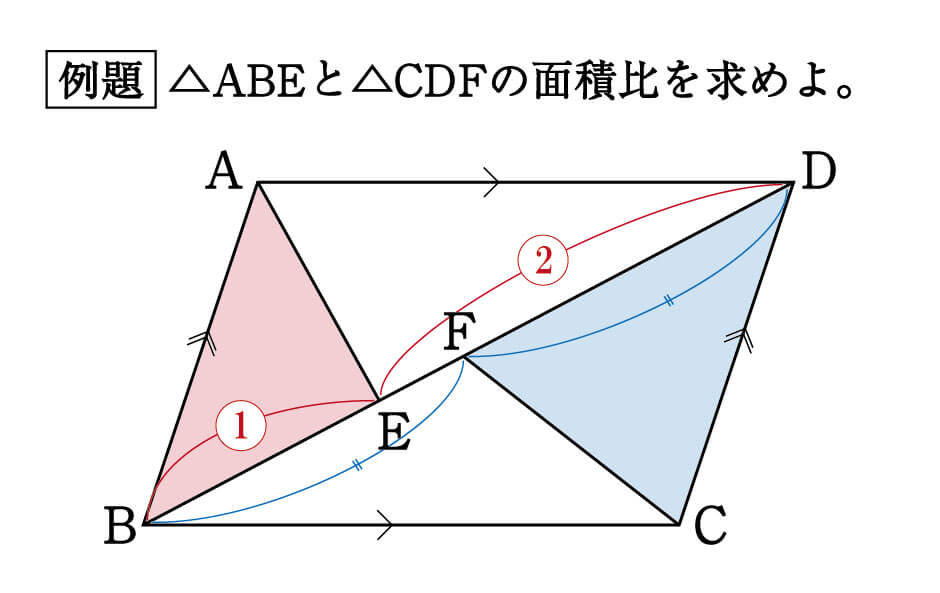



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



平行四辺形の性質1




A D 4 Abcd E H F Bee Descubre Como Resolverlo En Qanda
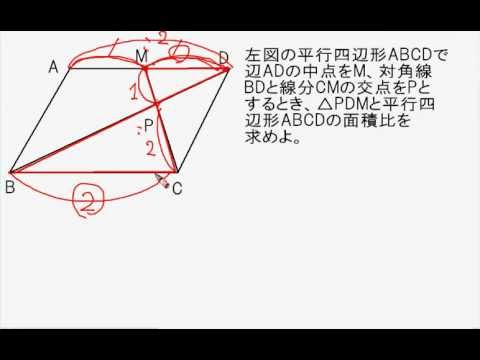



ご質問への解説 平行四辺形面積比 Youtube



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ
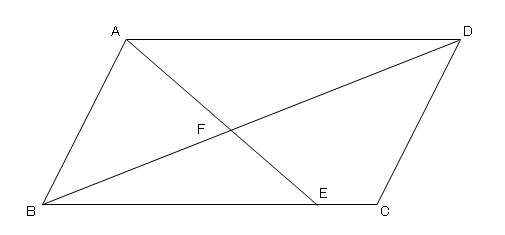



相似と線分の比 4 ネット塾
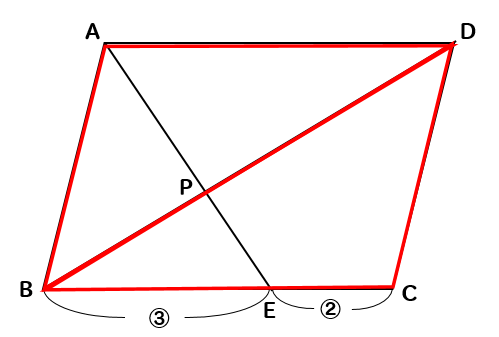



相似 平行四辺形と面積比の問題を徹底解説 数スタ



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ



0 件のコメント:
コメントを投稿